Xavier Décoret
The distance between a point ![]() and a line
and a line ![]() is defined as the
smallest distance between any point
is defined as the
smallest distance between any point ![]() on the line and
on the line and ![]() :
:
The manhattan distance between two points is defined as:
The question is then ``what is the formula that gives the manhattan distance between a point and a line?''.
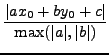 |
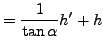 |
Next, we need to compute the two distances. For the horizontal one, we must solve: